
mlim
: Single and Multiple Imputation with Automated Machine Learningmlim is the first missing data
imputation software to implement automated machine learning for
performing multiple imputation or single imputation of
missing data. The software, which is currently implemented as an R
package, brings the state-of-the-arts of machine learning to provide a
versatile missing data solution for various data types (continuous,
binary, multinomial, and ordinal). In a nutshell,
mlim is expected to outperform any other
available missing data imputation software on many grounds. For example,
mlim is expected to deliver:
mlim excells in making an efficient use of
available CPU cores and the runtime scales fairly well as the size of
data becomes huge.The high performance of mlim is mainly
by fine-tuning an ELNET
algorithm, which often outperforms any standard statistical procedure or
untuned machine learning algorithm and generalizes very well. However,
mlim is an active research project and
hence, it comes with a set of experimental optimization
toolkit for exploring the possibility of performing multiple
imputation with industry-standard machine learning algorithms such as
Deep Learning, Gradient Boosting Machine, Extreme
Gradient Boosting, and Stacked Ensembles. These algorithms
can be used for either imputing missing data or optimizing already
imputed data, but are NOT used by default NOR recommended to all
users. Advanced users who are interested in exploring the
possibilities of imputing missing data with these algorithms are
recommended to read the free handbook (see below). These algorithms, as
noted, are experimental, and the author is intended to examine their
effectiveness for academic research (at this point). If you are
interested to collaborate, get in
touch with the author.
NOTE: Prior to version 0.3.0,
mlimdid not use a stochastic procedure and thus, the multiple imputation algorithm was inflating the relationships between the imputed variables. A solution is implemented in version 0.3.0, which is automatically activated for multiple imputation and is currently under testing. You can investigate the code forstochastic = TRUEargument to see how this procedure is implemented. In stochastic multiple imputation,mlimuses the estimated RMSE of each continuous variable as an indication of standard error and replaces the imputed values with stochastic values drawn with a mean equal to the imputed value and SD equal to the RMSE. For factor variables, however,mlimdraws a random value based on estimated probabilities of each factor level for each missing value. These two procedures are still under testing… Meanwhile, for a single imputation,mlimcontinues to be the top performer among other R packages that I have tested.
Simply put, for each variable in the dataset,
mlim automatically fine-tunes a fast
machine learning model, which results in significantly lower imputation
error compared to classical statistical models or even untuned machine
learning imputation software that use Random Forest or unsuperwised
learning algorithms. Moreover, mlim is
intended to give social scientists a powerful solution to their missing
data problem, a tool that can automatically adopts to different variable
types, that can appear at different rates, with unknown destributions
and have high correlations or interactions with one another. But
it is not just about higher accuracy! mlim also delivers
fairer imputation, particularly for categorical and ordinal variables
because it automatically balances the levels of the avriable, minimizing
the bias resulting from class imbalance, which can often be seen in
social science data and has been commonly ignored by missing data
imputation software.
mlim outperforms other R packages for
all variable types, continuous, binary (factor), multinomial (factor),
and ordinal (ordered factor). The reason for this improved performance
is that mlim:
When a dataframe with NAs is given to
mlim, the NAs are replaced with plausible
values (e.g. Mean and Mode) to prepare the dataset for the imputation,
as shown in the flowchart below:
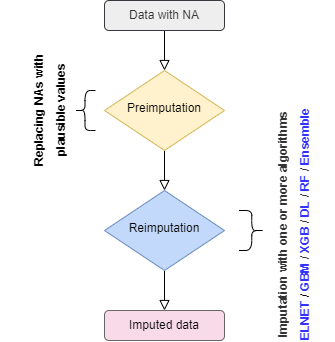
mlim follows three steps to optimize
the missing data imputation. This procedure is optional,
depending on the amount of computing resources available to you. In
general, ELNET imputation already
outperforms other available single and multiple imputation methods
available in R. However, the imputation error can be
further improved by training stronger algorithms such as
GBM, XGB,
DL, or even
Ensemble, stacking several models on top
of one another. For the majority of the users, the
GBM or XGB
(XGB is available only in Mac OSX and Linux) will significantly imprive
the ELNET imputation, if long-enough time
is provided to generate a lot of models to fine-tune them.

You do not necessarily need the post-imputation. Once you have
reimputed the data with ELNET, you can stop there.
ELNET is relatively a fast algorithm and it is easy to
fine-tune it compared to GBM, XGB,
DL, or Ensemble. In addition,
ELNET generalizes nicely and is less prone to overfiting.
In the flowchart below the procedure of mlim algorithm
is drawn. When using mlim, you can use
ELNET to impute a dataset with NA or optimize the imputed
values of a dataset that is already imputed. If you wish to go the extra
mile, you can use heavier algorithms as well to activate the
postimputation procedure, but it is strictly optional and by default,
mlim does not use postimputation.
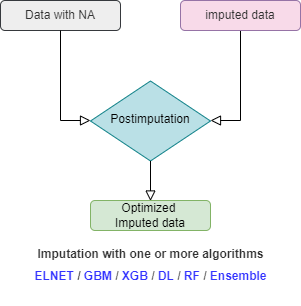
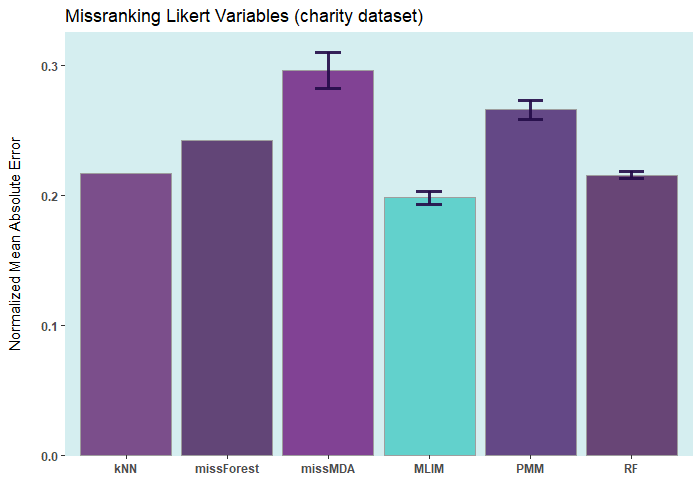
ELNET (without
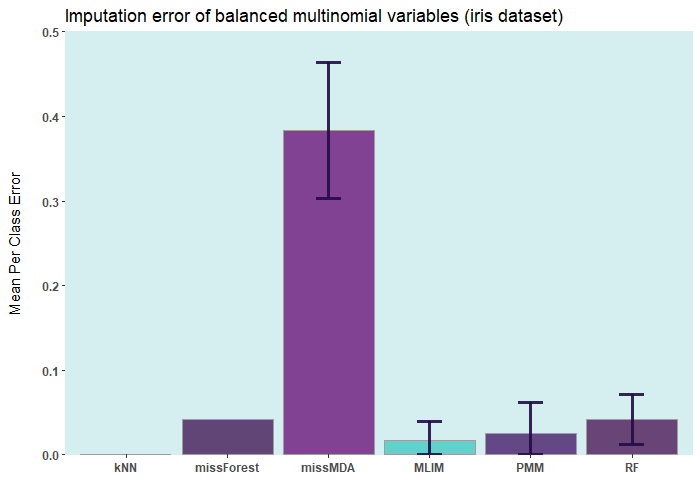
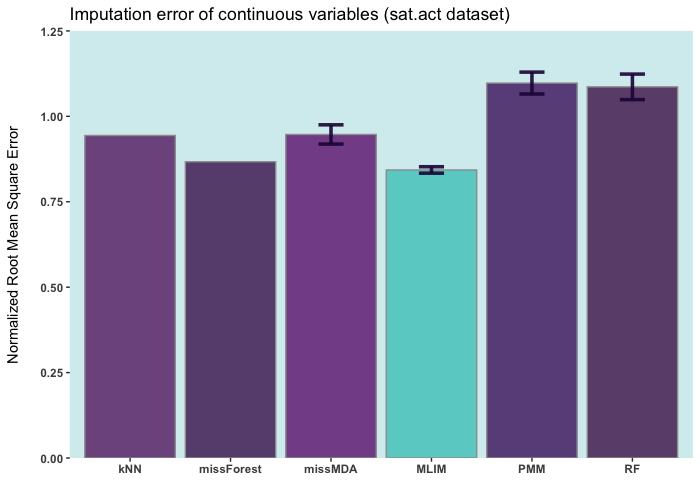
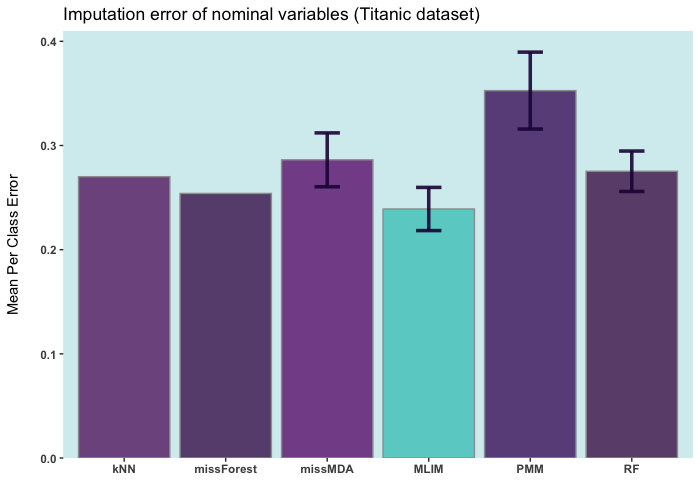
postimputation)Below are some comparisons between different R packages for carrying
out multiple imputations (bars with error) and single imputation. In
these analyses, I only used the ELNET
algorithm, which fine-tunes much faster than other algorithms
(GBM,
XGBoost, and
DL). As it evident,
ELNET already outperforms all other single
and multiple imputation procedures available in R
language. However, the performance of mlim
can still be improved, by adding another algorithm, which activates the
postimputation procedure.


mlim is under fast development. The
package receive monthly updates on CRAN. Therefore, it is recommended
that you install the GitHub version until version 0.1 is released. To
install the latest development version from GitHub:
library(devtools)
install_github("haghish/mlim")Or alternatively, install the latest stable version from CRAN:
install.packages("mlim")mlim supports several algorithms:
ELNET (Elastic Net)RF (Random Forest and Extremely Randomized Trees)GBM (Gradient Boosting Machine)XGB (Extreme Gradient Boosting, available in Mac OS and
Linux)DL (Deep Learning)Ensemble (Stacked Ensemble)
ELNETis the default imputation algorithm. Among all of the above, ELNET is the simplest model, fastest to fine-tune, requires the least amount of RAM and CPU, and yet, it is the most stable one, which also makes it one of the most generalizable algorithms. By default,mlimuses onlyELNET, however, you can add another algorithm to activate the post-imputation procedure.
GBM vs ELNETBut which one should you choose, assuming computation resources are
not in question? Well, GBM is very liokely
to outperform ELNET, if you specify a
large enough max_models argument to well-tune the algorithm
for imputing each feature. That basically means generating more than 100
models, at least. But you will enjoy a slight – yet probably
statistically significant – improvement in the imputation accuracy. The
option is there, for those who can use it, and to my knowledge,
fine-tuning GBM with large enough number
of models will be the most accurate imputation algorithm compared to any
other procedure I know. But ELNET comes
second and compared to its speed advantage, it is indeed charming!
Both of these algorithms offer one advantage over all the other
machine learning missing data imputation methods such as kNN, K-Means,
PCA, Random Forest, etc… Simply put, you do not need to specify any
parameter yourself, everything is automatic and
mlim searches for the optimal parameters
for imputing each variable within each iteration. For all the
aformentioned packages, some parameters need to be specified, which
influence the imputation accuracy. Number of k for kNN, number
of components for PCA, number of trees (and other parameters) for Random
Forest, etc… This is why elnet outperform the other
packages. You get a software that optimizes its models on its own.
mlim fine-tunes models for imputation,
a procedure that has never been implemented in other R packages. This
procedure often yields much higher accuracy compared to other machine
learning imputation methods or missing data imputation procedures
because of using more accurate models that are fine-tuned for each
feature in the dataset. The cost, however, is computational resources.
If you have access to a very powerful machine, with a huge amount of RAM
per CPU, then try GBM. If you specify a
high enough number of models in each fine-tuning process, you are likely
to get a more accurate imputation that
ELNET. However, for personal machines and
laptops, ELNET is generally recommended
(see below). If your machine is not powerful enough, it is
likely that the imputation crashes due to memory problems…. So,
perhaps begin with ELNET, unless you are
working with a powerful server. This is my general advice as long as
mlim is in Beta version and under
development.
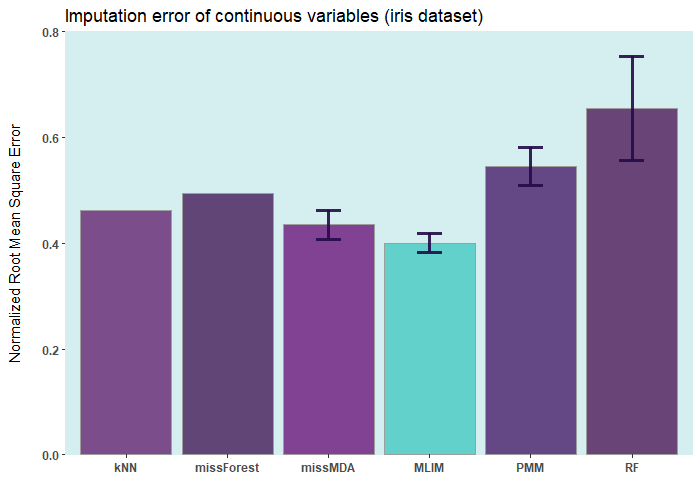
iris ia a small dataset with 150 rows only. Let’s add
50% of artifitial missing data and compare several state-of-the-art
machine learning missing data imputation procedures.
ELNET comes up as a winner for a very
simple reason! Because it was fine-tuned and all the rest were not. The
larger the dataset and the higher the number of features, the difference
between ELNET and the others becomes more
vivid.
In a single imputation, the NAs are replaced with the most plausible
values according the model. You do not get the diversity of the multiple
imputation, but you still get an estimated imputation error based on
10-fold (or higher, if specified) cross-validation procedure for each
variable (column) in the dataset. As shown below, mlim
provides the mlim.error() function to
summarize the imputation error for the entire dataset or each
variable.
# Comparison of different R packages imputing iris dataset
# ===============================================================================
rm(list = ls())
library(mlim)
library(mice)
library(missForest)
library(VIM)
# Add artifitial missing data
# ===============================================================================
irisNA <- mlim.na(iris, p = 0.5, stratify = TRUE, seed = 2022)
# Single imputation with mlim, giving it 180 seconds to fine-tune each imputation
# ===============================================================================
MLIM <- mlim(irisNA, m=1, seed = 2022, tuning_time = 180)
print(MLIMerror <- mlim.error(MLIM, irisNA, iris))
# kNN Imputation with VIM
# ===============================================================================
kNN <- kNN(irisNA, imp_var=FALSE)
print(kNNerror <- mlim.error(kNN, irisNA, iris))
# Single imputation with MICE (for the sake of demonstration)
# ===============================================================================
MC <- mice(irisNA, m=1, maxit = 50, method = 'pmm', seed = 500)
print(MCerror <- mlim.error(MC, irisNA, iris))
# Random Forest Imputation with missForest
# ===============================================================================
set.seed(2022)
RF <- missForest(irisNA)
print(RFerror <- mlim.error(RF$ximp, irisNA, iris))mlim supports multiple imputation. All you need to do is
to specify an integer higher than 1 for the value of m. For
example, set m = 5 in the mlim function to
impute 5 datasets. Then, mlim returns a list including 5
datasets. You can convert this list to a mids object using
the mlim.mids() function and then follow
up the analysis with the mids object the same way it is
carried out by the mice R
package. Here is an example:
# Comparison of different R packages imputing iris dataset
# ===============================================================================
rm(list = ls())
library(mlim)
library(mice)
# Add artifitial missing data
# ===============================================================================
irisNA <- mlim.na(iris, p = 0.5, stratify = TRUE, seed = 2022)
# multiple imputation with mlim, giving it 180 seconds to fine-tune each imputation
# ===============================================================================
MLIM2 <- mlim(irisNA, m = 5, seed = 2022, tuning_time = 180)
print(MLIMerror2 <- mlim.error(MLIM2, irisNA, iris))
mids <- mlim.mids(MLIM2, dfNA)
fit <- with(data=mids, exp=glm(Species ~ Sepal.Length, family = "binomial"))
res <- mice::pool(fit)
summary(res)