sasfunclust

The package sasfunclust implements the sparse and smooth functional clustering (SaS-Funclust) method proposed by Centofanti et al. (2021). SaS-Funclust is a new method for clustering functional data that aims to classify a sample of curves into homogeneous groups while jointly detecting the most informative portions of domain. The method relies on a general functional Gaussian mixture model whose parameters are estimated by maximizing a log-likelihood function penalized with the functional adaptive pairwise fusion penalty (FAPFP) and a roughness penalty. The package comprises two main functions and . The former performs the SaS-Funclust for fixed number of clusters G, tuning parameter of the smoothness penalty λ_s, and tuning parameter of the FAPFP λ_l. The latter executes the K-fold cross-validation procedure described in Centofanti et al. (2021) to choose G, λ_s, and λ_l.

Installation

The development version can be installed from GitHub with:

# install.packages("devtools")
devtools::install_github("unina-sfere/sasfunclust")

Example

This is a basic example which shows you how to apply the two main functions sasfclust and sasfclust_cv on a synthetic dataset generated as described in the simulation study of Centofanti et al. (2021).

We start by loading and attaching the sasfunclust package.

library(sasfunclust)

Then, we generate the synthetic dataset as follows.

n_i=20
train<-simulate_data("Scenario I",n_i=n_i,var_e = 1,var_b = 0.5^2)

To apply sasfclust_cv, sequences of G, λ_s, and λ_l should be defined.

lambda_s_seq=10^seq(-4,-3)
lambda_l_seq=10^seq(0,3)
G_seq=2

And, then, sasfclust_cv is executed.

mod_cv<-sasfclust_cv(X=train$X,grid=train$grid,G_seq=G_seq,
lambda_l_seq = lambda_l_seq,lambda_s_seq =lambda_s_seq,maxit = 50,K_fold = 5,q=30,ncores = 7)

The results are plotted.

plot(mod_cv)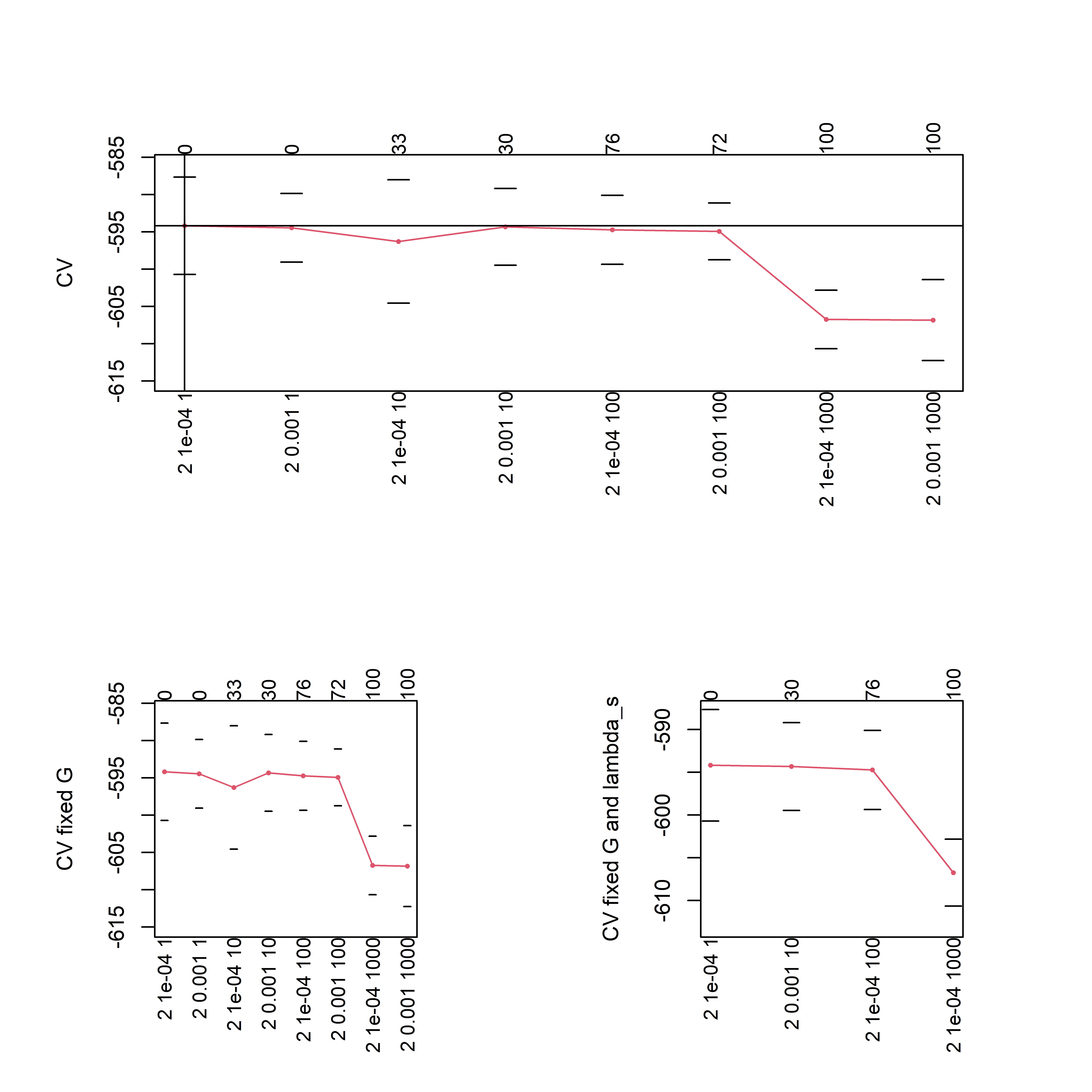

By using the model selection method described in Centofanti et al. (2021), the optimal values of G, λ_s, and λ_l, are 2, 10^− 4, and 10², respectively.

Finally, sasfclust is applied with G, λ_s, and λ_l fixed to their optimal values.

mod<-sasfclust(X=train$X,grid=train$grid,G=mod_cv$G_opt,
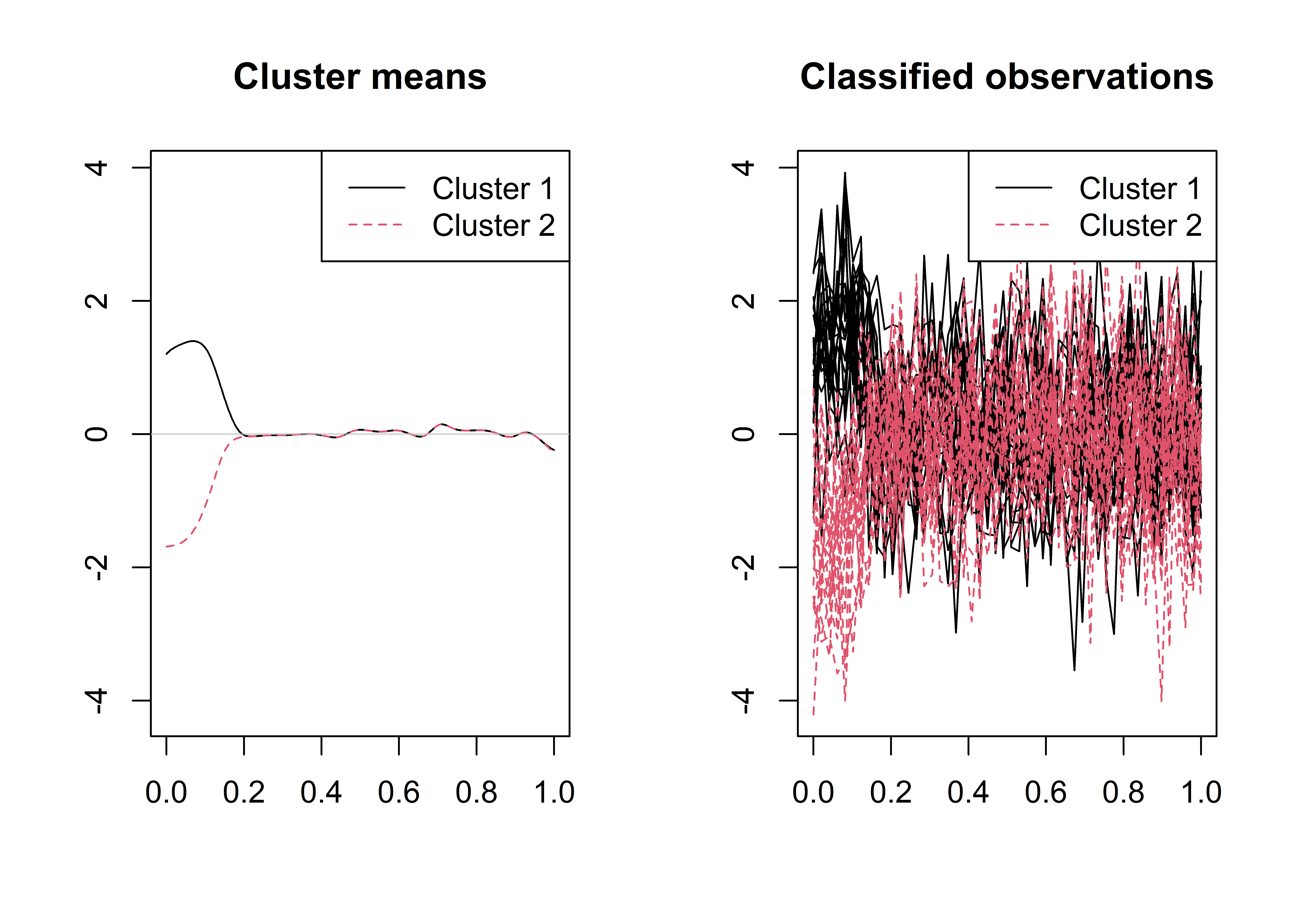
lambda_l = mod_cv$lambda_l_opt,lambda_s =mod_cv$lambda_s_opt,maxit = 50,q=30)

The cluster membership vector and the plot of the estimated cluster mean functions and the classified curves are obtained as follows.

print(mod$clus$classes)
plot(mod)

References

• Centofanti, F., Lepore, A., & Palumbo, B. (2021). Sparse and Smooth Functional Data Clustering. arXiv preprint arXiv:2103.15224.